Introduction
Some days in theoretical physics feel like mountain climbing. You spend hours inching upward through algebra, you finally reach a viewpoint, and the “beautiful simple formula” everyone promised turns out to be hiding behind a boulder labeled “one more identity.”
Then there are days when a language model strolls by, points at your pile of terms, and says, calmly, “This cancels.”
That’s the core of the 2026 ChatGPT Physics story: an OpenAI-backed preprint on arXiv argues that a class of gluon scattering amplitudes long treated as zero can be nonzero, but only in a tightly defined corner of kinematics. It is not a new particle. It is not a rewrite of QCD. It is a loophole in an argument, plus a compact formula that appears once you stand in exactly the right place.
If you’ve seen headlines that sound like “GPT-5.2 discovered new physics,” this is your time-saving translation. We’ll pin down the claim, the caveat, the verification checks, and what this does, and does not, change about physics and about ChatGPT Physics as a tool.
Table of Contents
1. ChatGPT Physics, Meet Reality: What Happened In The GPT-5.2 Preprint
The paper’s title is refreshingly blunt: “Single-minus gluon tree amplitudes are nonzero.” That lands because many of us learned the opposite as a reflex. Single-minus at tree level, one negative-helicity gluon and the rest positive, is “supposed” to vanish.
The authors show the usual argument assumes generic momenta. Move onto a special slice of momentum space called the half-collinear regime, and the argument breaks. Then the amplitude does not have to be zero, and in a particular channel they give an all-n closed form and test it with standard consistency checks.
| What People Heard | What The Paper Says | Why It Matters |
|---|---|---|
| “GPT-5.2 found new physics” | A tree-level gluon amplitude previously treated as zero becomes nonzero under half-collinear or complexified kinematics. | It refines a “zero” rule by exposing an assumption, and adds a compact formula in a neglected regime. |
| “The Standard Model was wrong” | The textbook reasoning still holds for generic kinematics. | The win is precision, not overthrow. |
| “LLMs are doing science now” | GPT-5.2 Pro conjectured the all-n pattern, then a scaffolded internal model produced a proof, and humans verified it with known checks. | The workflow is a template: compute, simplify, conjecture, verify. |
1.1 What You’ll Learn
- The one-sentence claim and the one-sentence caveat
- Why “single-minus” was expected to be zero
- What “half-collinear” means, in geometry terms
- The verification hooks, Berends–Giele recursion and Weinberg soft theorem
- How to use ChatGPT Physics without fooling yourself
1.2 Who Wrote It, And Why The Names Matter
This is not a random blog post with a spicy title. The author list includes Alfredo Guevara, Alexandru Lupsasca, David Skinner, Andrew Strominger, and Kevin Weil on behalf of OpenAI, and it sits on arXiv as 2602.12176v1.
That mix is relevant because it signals intent. This is an amplitudes paper that happens to have a model in the loop, not a model demo that happens to mention amplitudes. The safest mental stance is: take the physics as physics, then evaluate the AI method on whether it helped them do physics faster.
2. The One-Sentence Claim, And The One-Sentence Caveat
The claim: single-minus gluon tree amplitudes can be nonzero.
The caveat: they become nonzero only when the external momenta obey special half-collinear conditions, or when you allow complexified momenta where similar degeneracies can live.
If you want the news-cycle keywords in one place, this is the gpt 5.2 physics headline: the gpt-5.2 theoretical physics chatter is about a gpt-5.2 physics paper proposing a gpt-5.2 new physics result that is narrow, technical, and testable.
ChatGPT Physics did not “break” physics. It tightened a statement that was always meant to be read with an implicit “for generic kinematics.”
3. What A Scattering Amplitude Is, Only The Bits You Need
A scattering amplitude is the object you compute when you want the quantum probability for particles to come in one way and leave another way. It’s the bridge between your theory and your predictions.
Tree level means no loops, just the simplest diagrams. It’s also where the surprise tends to show up, because many complicated intermediate expressions collapse into simple final answers.
For gluons, the archetype is the Parke–Taylor formula for MHV amplitudes, the one that turns factorial-looking complexity into a single line. That’s why amplitude people perk up when ChatGPT Physics appears in the same paragraph as “new closed form.”
4. Why Physicists Expected “Single-Minus” To Be Zero
Single-minus means n gluons, one with negative helicity, n−1 with positive helicity. Helicity is the spin label that makes some amplitudes gorgeous and others a tax audit.
4.1 The Hidden Assumption: Generic Momenta
The standard “zero” argument is a gauge-choice and power-counting story. Pick polarization vectors. Choose a reference spinor that makes the plus-helicity polarizations orthogonal, so their contractions vanish. Then count momentum factors available from vertices. At tree level you run out, so the amplitude looks forced to be zero.
The loophole is surgical: that reference choice fails when certain spinor brackets vanish. On the relevant kinematic walls, the “convenient” polarization choice becomes singular. Once the proof is gone, the amplitude is free to be nonzero.
This is the first place the ChatGPT Physics narrative can mislead. The old argument was never wrong, it was conditional.
5. The Half-Collinear Regime Explained, No Mysticism, Just Geometry

Half-collinear is not vibes. It’s a locus defined by setting all angle brackets ⟨ij⟩ to zero, while allowing square brackets [ij] to remain nonzero in a signature where that’s consistent. In the paper’s language, this can be realized in Klein signature or via complexified momenta.
5.1 A Useful Mental Picture
Think of momentum space as a high-dimensional room. Generic kinematics is the interior. Half-collinear is a thin wall. You do not hit it by accident, but you can stand on it deliberately, and when you do, statements that were true in the room need to be re-checked on the wall.
On that wall, the usual “make everything orthogonal” trick can blow up. That’s why the half-collinear regime gluon amplitude story is logically allowed.
5.2 Chambers, Walls, And Why Piecewise-Constant Is A Feature
Once you restrict to this slice, the amplitude doesn’t vary smoothly with momenta the way you might expect from everyday physics intuition. Instead, it can become piecewise constant across “chambers,” and it jumps when you cross codimension-one “walls” defined by sign changes of certain brackets.
That sounds odd until you remember what’s happening. You are not exploring the full, generic kinematic space. You are living on a constrained surface with distributional support. On that surface, discrete-looking behavior is less mysterious and more like a map with regions separated by sharp borders.
6. What’s Actually New Here, And What People Confuse It With
Let’s deflate the meme version first.
6.1 Not A New Particle, Not A New Force
This is tree-level Yang–Mills theory. Same gluons. Same interactions. Same QCD backbone. Nobody is proposing a new term in the Standard Model.
6.2 A Refined Statement About A “Zero”
The novelty is the explicit, constructive statement: “Single-minus gluon tree amplitudes are nonzero” once you specify the half-collinear regime and a particular channel. That’s the exact phrase, and it’s doing real work.
6.3 A Compact All-n Formula In A Special Channel
In the paper’s restricted region, the stripped amplitude becomes piecewise constant and only takes values in {−1, 0, 1}. They present a clean product form for all n. That’s the kind of simplicity that tends to unlock more questions than it answers.
6.4 Why People Keep Saying “Wasn’t This Known?”
This subfield has a long memory. There are earlier hints in twistor space and self-dual Yang–Mills discussions that single-minus configurations can have support in degenerate kinematics. What feels different here is the concrete, closed-form expression you can plug into recursion checks, plus a method that produces an all-n pattern instead of a collection of one-off special cases.
ChatGPT Physics is the catalyst, but the object is the point: a compact expression you can actually use.
7. What GPT-5.2 Did Vs What The Humans Did, Step By Step
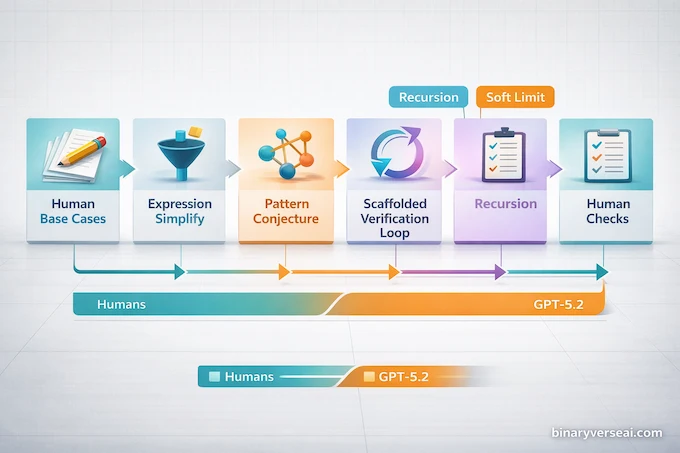
This is the part that feels most “2026” to me.
7.1 Humans: Messy Base Cases
The authors compute explicit cases up to n = 6. Even there, the expressions get unwieldy. This is normal in amplitudes work. Intermediate forms can be absurd even when the final answer is simple.
7.2 ChatGPT Physics: Simplify, Then Conjecture
GPT-5.2 Pro is reported to have simplified those base cases into much shorter expressions, then spotted the pattern and conjectured the all-n formula that appears as Eq. (39).
That’s not magic. It’s accelerated pattern recognition on top of human-computed ground truth.
7.3 Scaffolded Loop: The Long Verification Grind
Then an internal scaffolded model ran a long reasoning loop, produced the same formula, and generated a proof route. The paper frames this as a long-running verification loop, not a moment of inspiration, and that distinction matters.
If you’ve ever tried to prove an identity that “obviously should be true,” you know the grind. You chase sign conventions. You realize a limit has to be taken in the right order. You discover a hidden factor of two. A scaffolded system is valuable precisely because it can keep pushing through that grind without drifting into story-telling.
7.4 Humans: Kill The Result With Known Checks
Finally, the humans verify. If you work in amplitudes, you already know the two tests that matter most: does it satisfy Berends–Giele recursion, and does it behave correctly in soft limits.
8. “How Do We Know It’s Not Hallucination?” The Verification Checklist
The right skepticism is operational: what would falsify this, and did they test it.
The paper emphasizes checks that amplitudes people actually trust, including Berends–Giele recursion and the soft theorem / Weinberg soft theorem, plus structural identities like cyclicity and Kleiss–Kuijf relations.
| Check | What It Tests | Why It’s Meaningful |
|---|---|---|
| Berends–Giele recursion | Whether the closed form satisfies the standard recursive construction of tree amplitudes. | Wrong patterns tend to break fast when you recurse. |
| Soft theorem, Weinberg soft theorem | Whether the amplitude behaves correctly when one gluon becomes soft. | Soft limits are rigid constraints, like unit tests for the infrared. |
| Cyclicity, KK relations, U(1) decoupling | Whether the color-ordered structure and identities hold. | These are structural symmetries, easy to audit. |
8.1 Two Practical Verification Hooks
If you want a mental checklist for results like this, steal the authors’ hooks. Berends–Giele recursion is the build-it-from-smaller-parts test. The soft theorem is the take-a-particle-to-zero-momentum test. Passing both does not make a result true by decree, but failing either usually kills it immediately.
ChatGPT Physics earns credibility here because it is boxed into constraints that don’t care about eloquence. This is the version of ChatGPT Physics you can actually trust.
8.2 A Quick Glossary For The Long-Tail Terms
- Single-minus gluon tree amplitudes: tree-level scattering amplitudes with one minus-helicity gluon and the rest plus.
- Half-collinear regime: special kinematics where ⟨ij⟩ vanish, enabling degenerate support.
- Berends–Giele recursion: a constructive recursion that builds multi-leg tree amplitudes from smaller blocks.
- Weinberg soft theorem: the constraint on amplitudes when one particle’s momentum becomes soft.
9. The Skeptic’s Corner: “Isn’t This Just Mathematica On A Bigger GPU?”
It’s a fair question, and the answer is subtle.
Simplification in amplitudes is not cosmetic. When a combinatorial mess collapses into a product of sign factors, it often signals the right variables, the right kinematic chamber, or both. You can get there with traditional CAS tools, but you often need to know what you are looking for.
A scaffolded model’s advantage is that it will try more compressions and more pattern hypotheses than a tired human, then hand you a candidate that you can hammer with standard checks. The scientific value is not the CPU time, it’s the speed of the conjecture loop.
That’s why the workflow, conjecture → verify → extend, is the headline. ChatGPT Physics is acting like a search strategy across expression space.
10. What This Could Unlock Next, Gravitons, Extensions, And Why People Care
Why should anyone care about a weird kinematic wall?
Because simple formulas are portals. The paper notes the construction generalizes from gluons to gravitons, and gestures at broader structures and symmetry questions.
This is why people keep repeating Parke–Taylor as an analogy. Parke–Taylor did not just shorten algebra. It reorganized a field’s instincts.
No, this is not Parke–Taylor 2.0. But it is the same pattern: find a surprising pocket of simplicity, verify it with boring tests, then see what that pocket is trying to teach you.
ChatGPT Physics fits cleanly into that tradition.
11. What This Means For ChatGPT Physics Users, Homework Vs Research
Here’s the clean truth: research-grade scaffolding is not the same as everyday chat.
In the preprint, ChatGPT Physics sits inside a long-running verification loop. In a normal chat window, you are the loop. That’s why “chatgpt physics solver” results online can swing from impressive to nonsense. The model is not inconsistent, the workflow is.
So, is chatgpt good at physics? Yes, when you use it like a junior collaborator with unlimited patience and zero authority.
11.1 A Minimal “Don’t Fool Yourself” Workflow
- Write the assumptions first, then ask.
- Ask for the derivation, not just the answer.
- Demand at least one verification hook: a symmetry, a limit, or a recursion relation.
- Recompute one small special case yourself.
That is basically what the authors did, scaled down to human life.
11.2 The Real Lesson
The best way to read this story is not “LLM does physics.” It’s “verification harness makes conjecturing cheap.” That future version of ChatGPT Physics is the one worth paying attention to.
If you want to go deeper, read the arXiv preprint, then do the one exercise that turns headlines into understanding: pick a tiny n, trace the usual zero-proof, and watch exactly where it fails when you slide into the half-collinear regime.
If you like these time-respecting breakdowns of ChatGPT Physics, share this post with your most skeptical friend, and drop a comment with the next paper you want dissected.
1: Is ChatGPT good at physics?
Yes, for many structured problems and explanations. But this ChatGPT Physics headline result is not “normal ChatGPT doing homework.” The GPT-5.2 work used research-grade scaffolding, long runtimes, and expert verification, which is a different workflow than everyday Q&A.
2: How is AI used in physics?
Most often it helps with symbolic manipulation, pattern finding, simulation acceleration, and data analysis. In the ChatGPT Physics preprint story, the key loop is simple and powerful: generate a conjecture, then test it against known consistency checks, then let humans validate what survives.
3: Did GPT-5.2 really discover “new physics,” or just simplify math?
The clean framing: it helped derive a closed-form expression in a regime where the “zero” assumption was too broad, then the result was checked against standard amplitude constraints. The hype framing (“AI found a new particle”) is wrong. The useful framing is “AI helped find structure, humans verified it.”
4: What is the half-collinear regime (in plain English)?
It’s a special alignment of particle momenta. Many “must be zero” arguments assume generic momenta. In this precisely defined slice of momentum space, those assumptions break, and the amplitude can be nonzero without breaking consistency.
5: Is there any AI for physics problem solving (a “physics solver”)?
Yes, including dedicated chatgpt physics solver workflows. They can be great for practice and structured steps. For accuracy, you still need clear assumptions, unit checks, and independent verification for anything that matters, especially for open-ended or underspecified problems.

