1. Why This Experiment Matters
If you care about chat gpt mathematics, this is the study that deserves your full attention. In late August 2025, a viral post claimed GPT-5 improved a classic convex optimization bound in minutes. Flashy, yes. Verifiable, not quite. A trio of probabilists decided to test something concrete instead, and the result is the cleanest look yet at GPT-5 reasoning on real math. They asked the model to turn a known, qualitative theorem into a quantitative one with an explicit convergence rate. That is the sort of upgrade that separates clever pattern matching from research-grade insight.
The paper lives at the intersection of Malliavin calculus and Stein’s method. That sounds esoteric, and it is, but the question is simple. Can chat gpt mathematics move from “this converges” to “this converges at this specific rate,” then hold up under proof checking. The answer, in brief, is promising and human-dependent.
Table of Contents
2. The Setup

The authors chose a setting they know inside out, the Malliavin–Stein framework for central limit theorems. They started with a recent qualitative result and asked GPT-5 to produce a quantitative refinement in total variation distance. That means they wanted an explicit bound on how close a normalized random variable is to a true Gaussian. This is not symbolic algebra. It tests GPT-5 reasoning across definitions, identities, and parity constraints, the kind of careful thinking that decides whether chat gpt mathematics is an academic toy or a practical assistant.
The target was a two-chaos sum, a random variable Z built as X plus Y where X and Y live in different Wiener chaoses with different parities. This structure kills certain mixed odd moments, a crucial simplification that a system with real gpt-5 math ability must recognize and use.
3. A One-Line Punchline
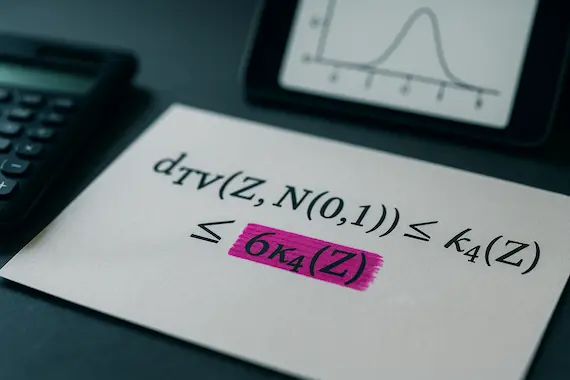
GPT-5, guided by the authors, reached a quantitative fourth-moment theorem. In plain language, if the fourth cumulant of Z is small, then Z is close to normal, and you even get a clean bound:
- Total variation distance between Z and N(0, 1) is at most the square root of six times the fourth cumulant of Z.
That single inequality packs a lot. It turns an existence claim into a numeric estimate you can check. It also anchors chat gpt mathematics in a space where error bars matter.
4. What GPT-5 Got Right
GPT-5 used the right tools for the Gaussian case. It leaned on the Malliavin derivative, the Ornstein–Uhlenbeck operator, and the contraction machinery for multiple integrals. It decomposed the hard part, a covariance term, into orthogonal chaos components, then tied everything back to fourth cumulants and parity. That is not button-pushing. That is structured, multi-step GPT-5 reasoning in a domain where small algebraic slips break the proof. It shows why chat gpt mathematics is no longer just “solve my homework” and is starting to look like AI for mathematics that a working researcher can actually use.
5. Where GPT-5 Tripped, And How It Recovered
On its first pass, GPT-5 proposed an incorrect formula for a key covariance term. Left unchecked, the proof would have collapsed. Once the authors challenged that step, the model revised the derivation and produced the correct identity. That is the honest picture. Chat gpt mathematics can reach the right hill, and it can climb most of it, yet it still stumbles on loose rocks. In the Poisson extension, the model initially missed that a covariance of squared terms stays nonnegative, a property available right in the cited literature. A nudge to the right equation number fixed the course. This is GPT-5 reasoning as a collaborative loop, not as an oracle.
6. The Poisson Side, With A Twist

The Poisson case mirrors the Gaussian analysis, yet it introduces a new variable. Mixed odd moments need not vanish. That difference matters. The authors lay out a variant of the theorem that still delivers Gaussian convergence for the two-chaos sum, provided those mixed odd terms fade. They also construct a crisp counterexample. You can match variance and even the fourth moment, and still fail to get a Gaussian limit, because the third moment refuses to die. That is a perfect teaching moment for chat gpt mathematics. Matching a handful of moments is not the whole story. Structure is.
7. A Quick Reference Table
| Setting | What Was Tested | Key Result | Where GPT-5 Stumbled | Human Input Required | Relevance to ChatGPT Mathematics |
|---|---|---|---|---|---|
| Gaussian two-chaos sum | Turn a qualitative CLT into a quantitative bound in total variation | A clean inequality that ties distance to normality to the fourth cumulant. This gives a usable convergence rate. | Wrong covariance expansion on first try, later corrected | Pinpoint the incorrect identity, request a detailed re-derivation, verify each contraction step | Shows chat gpt mathematics can scale from ideas to estimates when the structure is well chosen |
| Poisson two-chaos sum | Extend the approach to Poisson chaoses | A convergence result under vanishing mixed odd moments, plus a counterexample if they persist | Missed built-in positivity of a covariance until prompted | Direct the model to the exact formula and restate the theorem with the right hypothesis | Proves chat gpt mathematics needs guardrails where symmetry breaks |
8. What This Means For Researchers
The study’s most useful conclusion is not a math fact. It is a workflow fact. Working with GPT-5 felt like working with a strong junior assistant at project kickoff. The assistant can apply known tools, combine ideas across sources, and suggest plausible extensions. The assistant also makes subtle mistakes that require immediate checks. If you want chat gpt mathematics to save time, you invest time first, by lining up definitions, reminding the system of parity, and asking for expansions you can verify line by line. That is how AI for mathematics produces value.
This also reframes “best AI for mathematics.” It is not the one that spits out the cleverest lemma. It is the one that lets you steer, accepts correction, and stays consistent after edits. The paper shows GPT-5 can do that, which is why the term Math GPT is starting to feel less like a meme and more like a toolkit label.
9. The Real Gains, The Real Costs
There is real uplift. With the authors setting pace, GPT-5 produced a new quantitative bound for a structured problem and a Poisson analogue with a sharp counterexample. That is the kind of result OpenAI math skeptics have been asking for. At the same time, there is a predictable cost. Every line still needs verification. The model’s confidence is high even when a formula is off by a factor, and in this neighborhood a factor can void an argument. If chat gpt mathematics is going to be part of a serious proof, it must run inside a process that bakes in review from the first draft.
There is also an ecosystem risk. Once models can assemble incremental extensions on demand, we will see more of them. The paper names that risk directly. A flood of technically correct yet mildly interesting papers will make it harder for original work to stand out. That is not fatal to research. It is a reminder to choose problems where the structure resists copying and where GPT-5 reasoning helps expose real insight rather than just repackaging known machinery.
10. What To Do With This, If You Write Or Review Proofs
If you write proofs, the lesson is to design with constraints. Give the model the exact objects, the target functional distance, and the identities you want to see applied. Ask for the reduction to fourth cumulants, then require every term in the variance to be exposed and bounded. This is where chat gpt mathematics shines. It handles the bookkeeping and lets you focus on the key turns.
If you review, read with a new checklist. Look for parity claims. Look for the bridge from the Malliavin bound to total variation. Look for the contraction indices. If a covariance comparison shows up, check whether the expansion sits on the correct chaos orders. You will catch the same sorts of missteps the authors caught, and you will do it in minutes.
11. Why The Bound Matters Beyond This Paper
Bounds like the one in this study travel well. They plug into questions far beyond the specific chaos orders used here. If your model maps high-dimensional fields to scalars, total variation bounds give you a way to certify asymptotic normality with a number, not a shrug. That unlocks tighter error bars and cleaner comparisons. It also gives chat gpt mathematics a credible role in the daily work of AI solving math problems, where almost everything hinges on turning intuition into an inequality you can defend.
The Poisson counterexample is equally valuable. It shows where structure breaks. Matching variance and kurtosis is not enough. If a third moment keeps hiding in the sum, you will not get a Gaussian at the end. That story will repeat in other non-symmetric regimes. Keep it in mind when you ask a Math GPT to “generalize the argument.”
12. So, Can ChatGPT Really Do Math?
For everyday needs, yes, and it is getting fast. For research-grade work, the answer is more precise. With the right prompts and checks, GPT-5 converts a qualitative theorem into a quantitative one and helps extend the result to a new setting. That is a strong data point for gpt-5 math ability. The model reasons through definitions, applies the right identities, and corrects course when challenged. It does not replace the mathematician. It accelerates the parts that reward patience and structure. That is the win baked into chat gpt mathematics.
This should also reset the narrative about OpenAI math. The headline is not “AI solved an open problem.” The headline is “AI can help you produce verifiable, bounded results in areas where the machinery is heavy.” That is a more useful claim. It fits how real teams work. It also sets a higher bar for future models. When people ask for the best AI for mathematics, they will start to include traceable bounds and counterexamples in the definition.
13. Practical Prompts That Actually Worked
- State the exact target bound and the distance. Ask for total variation, not a vague norm.
- Name the objects with parity and order. Remind the model which mixed moments disappear.
- Demand a line-by-line variance decomposition before any inequality appears.
- When you see a key identity, ask for the contraction index and the chaos order of each term.
- If you suspect a sign, ask for the relevant line number or equation from the cited paper and make the model align to it.
These habits make chat gpt mathematics less about magic and more about reproducible scaffolding. They also make GPT-5 reasoning easier to audit, which is the only way it enters serious workflows.
14. The Bottom Line And A Simple Next Step
This paper shows a credible path for AI for mathematics. Choose problems with structure. Use GPT-5 to turn qualitative statements into quantitative ones. Keep humans in the loop at every algebraic hinge. Expect speed, not originality. Bring a reviewer’s eye from the first line. That is how chat gpt mathematics earns a desk in your lab.
If this resonates, try it on your own problem. Pick a known limit theorem in your domain. Ask GPT-5 to express the distance to the limit distribution in total variation and to bound it in terms of a small, interpretable statistic. Verify the contractions, the parities, and the covariance terms. Publish the bound only after you can defend each line. Then share what worked. Someone else will learn from your prompt engineering, and you will help push GPT-5 reasoning from novelty to standard practice.
1) Can ChatGPT-5 do high-level mathematics?
Yes, within a guided workflow. In a controlled Malliavin–Stein experiment, GPT-5 helped turn a qualitative theorem into a quantitative bound in total variation, then needed human correction when a key covariance step went wrong. This is the right way to use chat gpt mathematics, pair the model with expert review to turn ideas into verifiable steps.
2) Which version of ChatGPT is best for solving math problems?
For proof-style reasoning and research workflows, GPT-5 currently sets the pace in published testing. The study shows GPT-5 can apply the right tools, follow structure, and revise when challenged, which makes it the practical choice for chat gpt mathematics where you want traceable bounds and line-by-line checks. Human verification still matters.
3) Did GPT-5 actually solve a famous open problem in mathematics?
There was a widely shared claim that GPT-5-Pro improved a bound in convex optimization. Treat that as a claim on social media, not a peer-reviewed result. The paper you are covering offers the reliable evidence, a documented experiment where chat gpt mathematics produced a quantitative result under expert supervision.
4) How does GPT-5’s math ability compare to a human mathematician?
Think of GPT-5 as a strong junior assistant. It can combine known tools, propose directions, and carry a proof until a subtle error appears, then a human steps in to steer. That is the realistic takeaway for chat gpt mathematics, speed with structure, plus expert oversight for correctness.
5) What is the Malliavin-Stein method and why is it a good test for an AI?
Malliavin–Stein blends Malliavin calculus with Stein’s method to turn convergence statements into explicit error rates. It forces precise handling of cumulants, parity, and distances like total variation, which makes it an excellent stress test for chat gpt mathematics and for GPT-5 reasoning in particular.

